Module: transform¶
| skimage.transform.fast_homography | Projective transformation (homography). |
| skimage.transform.frt2(a) | Compute the 2-dimensional finite radon transform (FRT) for an n x n |
| skimage.transform.homography(image, H[, ...]) | Perform a projective transformation (homography) on an image. |
| skimage.transform.hough(img[, theta]) | Perform a straight line Hough transform. |
| skimage.transform.ifrt2(a) | Compute the 2-dimensional inverse finite radon transform (iFRT) for |
| skimage.transform.integral_image(x) | Integral image / summed area table. |
| skimage.transform.integrate(ii, r0, c0, r1, c1) | Use an integral image to integrate over a given window. |
| skimage.transform.iradon(radon_image[, ...]) | Inverse radon transform. |
| skimage.transform.probabilistic_hough(img[, ...]) | Performs a progressive probabilistic line Hough transform and returns the detected lines. |
| skimage.transform.radon(image[, theta]) | Calculates the radon transform of an image given specified projection angles. |
| skimage.transform.swirl(image[, center, ...]) | Perform a swirl transformation. |
| skimage.transform.warp(image, reverse_map[, ...]) | Warp an image according to a given coordinate transformation. |
fast_homography¶
- skimage.transform.fast_homography()¶
Projective transformation (homography).
Perform a projective transformation (homography) of a floating point image, using bi-linear interpolation.
For each pixel, given its homogeneous coordinate
![\mathbf{x}
= [x, y, 1]^T](../_images/math/1aa9d7913003fccfc89a3c2961147dac616653a4.png) , its target position is calculated by multiplying
with the given matrix,
, its target position is calculated by multiplying
with the given matrix, 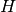 , to give
, to give 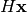 .
E.g., to rotate by theta degrees clockwise, the matrix should be
.
E.g., to rotate by theta degrees clockwise, the matrix should be[[cos(theta) -sin(theta) 0] [sin(theta) cos(theta) 0] [0 0 1]]
or, to translate x by 10 and y by 20,
[[1 0 10] [0 1 20] [0 0 1 ]].
Parameters : image : 2-D array
Input image.
H : array of shape (3, 3)
Transformation matrix H that defines the homography.
output_shape : tuple (rows, cols)
Shape of the output image generated.
order : int
Order of splines used in interpolation.
mode : {‘constant’, ‘mirror’, ‘wrap’}
How to handle values outside the image borders.
cval : string
Used in conjunction with mode ‘C’ (constant), the value outside the image boundaries.
frt2¶
- skimage.transform.frt2(a)¶
Compute the 2-dimensional finite radon transform (FRT) for an n x n integer array.
Parameters : a : array_like
A 2-D square n x n integer array.
Returns : FRT : 2-D ndarray
Finite Radon Transform array of (n+1) x n integer coefficients.
See also
- ifrt2
- The two-dimensional inverse FRT.
Notes
The FRT has a unique inverse iff n is prime. [FRT] The idea for this algorithm is due to Vlad Negnevitski.
References
[FRT] A. Kingston and I. Svalbe, “Projective transforms on periodic discrete image arrays,” in P. Hawkes (Ed), Advances in Imaging and Electron Physics, 139 (2006) Examples
Generate a test image: Use a prime number for the array dimensions
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
Apply the Finite Radon Transform:
>>> f = frt2(img)
Plot the results:
>>> import matplotlib.pyplot as plt >>> plt.imshow(f, interpolation='nearest', cmap=plt.cm.gray) >>> plt.xlabel('Angle') >>> plt.ylabel('Translation') >>> plt.show()
homography¶
- skimage.transform.homography(image, H, output_shape=None, order=1, mode='constant', cval=0.0)¶
Perform a projective transformation (homography) on an image.
For each pixel, given its homogeneous coordinate
![\mathbf{x}
= [x, y, 1]^T](../_images/math/1aa9d7913003fccfc89a3c2961147dac616653a4.png) , its target position is calculated by multiplying
with the given matrix,
, its target position is calculated by multiplying
with the given matrix, 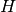 , to give
, to give 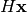 .
E.g., to rotate by theta degrees clockwise, the matrix should be
.
E.g., to rotate by theta degrees clockwise, the matrix should be[[cos(theta) -sin(theta) 0] [sin(theta) cos(theta) 0] [0 0 1]]
or, to translate x by 10 and y by 20,
[[1 0 10] [0 1 20] [0 0 1 ]].
Parameters : image : 2-D array
Input image.
H : array of shape (3, 3)
Transformation matrix H that defines the homography.
output_shape : tuple (rows, cols)
Shape of the output image generated.
order : int
Order of splines used in interpolation.
mode : string
How to handle values outside the image borders. Passed as-is to ndimage.
cval : string
Used in conjunction with mode ‘constant’, the value outside the image boundaries.
Examples
>>> # rotate by 90 degrees around origin and shift down by 2 >>> x = np.arange(9, dtype=np.uint8).reshape((3, 3)) + 1 >>> x array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=uint8) >>> theta = -np.pi/2 >>> M = np.array([[np.cos(theta),-np.sin(theta),0], ... [np.sin(theta), np.cos(theta),2], ... [0, 0, 1]]) >>> x90 = homography(x, M, order=1) >>> x90 array([[3, 6, 9], [2, 5, 8], [1, 4, 7]], dtype=uint8) >>> # translate right by 2 and down by 1 >>> y = np.zeros((5,5), dtype=np.uint8) >>> y[1, 1] = 255 >>> y array([[ 0, 0, 0, 0, 0], [ 0, 255, 0, 0, 0], [ 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]], dtype=uint8) >>> M = np.array([[ 1., 0., 2.], ... [ 0., 1., 1.], ... [ 0., 0., 1.]]) >>> y21 = homography(y, M, order=1) >>> y21 array([[ 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0], [ 0, 0, 0, 255, 0], [ 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]], dtype=uint8)
hough¶
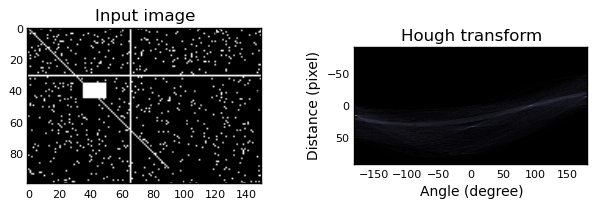
- skimage.transform.hough(img, theta=None)¶
Perform a straight line Hough transform.
Parameters : img : (M, N) ndarray
Input image with nonzero values representing edges.
theta : 1D ndarray of double
Angles at which to compute the transform, in radians. Defaults to -pi/2 .. pi/2
Returns : H : 2-D ndarray of uint64
Hough transform accumulator.
distances : ndarray
Distance values.
theta : ndarray
Angles at which the transform was computed.
Examples
Generate a test image:
>>> img = np.zeros((100, 150), dtype=bool) >>> img[30, :] = 1 >>> img[:, 65] = 1 >>> img[35:45, 35:50] = 1 >>> for i in range(90): >>> img[i, i] = 1 >>> img += np.random.random(img.shape) > 0.95
Apply the Hough transform:
>>> out, angles, d = hough(img)
Plot the results:
>>> import matplotlib.pyplot as plt >>> plt.imshow(out, cmap=plt.cm.bone) >>> plt.xlabel('Angle (degree)') >>> plt.ylabel('Distance %d (pixel)' % d[0]) >>> plt.show()
import numpy as np import matplotlib.pyplot as plt from skimage.transform import hough img = np.zeros((100, 150), dtype=bool) img[30, :] = 1 img[:, 65] = 1 img[35:45, 35:50] = 1 for i in range(90): img[i, i] = 1 img += np.random.random(img.shape) > 0.95 out, angles, d = hough(img) plt.subplot(1, 2, 1) plt.imshow(img, cmap=plt.cm.gray) plt.title('Input image') plt.subplot(1, 2, 2) plt.imshow(out, cmap=plt.cm.bone, extent=(d[0], d[-1], np.rad2deg(angles[0]), np.rad2deg(angles[-1]))) plt.title('Hough transform') plt.xlabel('Angle (degree)') plt.ylabel('Distance (pixel)') plt.subplots_adjust(wspace=0.4) plt.show()
(Source code, png)
ifrt2¶
- skimage.transform.ifrt2(a)¶
Compute the 2-dimensional inverse finite radon transform (iFRT) for an (n+1) x n integer array.
Parameters : a : array_like
A 2-D (n+1) row x n column integer array.
Returns : iFRT : 2-D n x n ndarray
Inverse Finite Radon Transform array of n x n integer coefficients.
See also
- frt2
- The two-dimensional FRT
Notes
The FRT has a unique inverse iff n is prime. See [R50] for an overview. The idea for this algorithm is due to Vlad Negnevitski.
References
[R50] (1, 2) A. Kingston and I. Svalbe, “Projective transforms on periodic discrete image arrays,” in P. Hawkes (Ed), Advances in Imaging and Electron Physics, 139 (2006) Examples
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
Apply the Finite Radon Transform:
>>> f = frt2(img)
Apply the Inverse Finite Radon Transform to recover the input
>>> fi = ifrt2(f)
Check that it’s identical to the original
>>> assert len(np.nonzero(img-fi)[0]) == 0
integral_image¶
- skimage.transform.integral_image(x)¶
Integral image / summed area table.
The integral image contains the sum of all elements above and to the left of it, i.e.:
![S[m, n] = \sum_{i \leq m} \sum_{j \leq n} X[i, j]](../_images/math/60eb18acdabe921f0fcbc69cf1dfc9fe4934bb1d.png)
Parameters : x : ndarray
Input image.
Returns : S : ndarray
Integral image / summed area table.
References
[R51] F.C. Crow, “Summed-area tables for texture mapping,” ACM SIGGRAPH Computer Graphics, vol. 18, 1984, pp. 207-212.
integrate¶
- skimage.transform.integrate(ii, r0, c0, r1, c1)¶
Use an integral image to integrate over a given window.
Parameters : ii : ndarray
Integral image.
r0, c0 : int
Top-left corner of block to be summed.
r1, c1 : int
Bottom-right corner of block to be summed.
Returns : S : int
Integral (sum) over the given window.
iradon¶
- skimage.transform.iradon(radon_image, theta=None, output_size=None, filter='ramp', interpolation='linear')¶
Inverse radon transform.
Reconstruct an image from the radon transform, using the filtered back projection algorithm.
Parameters : radon_image : array_like, dtype=float
Image containing radon transform (sinogram). Each column of the image corresponds to a projection along a different angle.
theta : array_like, dtype=float, optional
Reconstruction angles (in degrees). Default: m angles evenly spaced between 0 and 180 (if the shape of radon_image is nxm)
output_size : int
Number of rows and columns in the reconstruction.
filter : str, optional (default ramp)
Filter used in frequency domain filtering. Ramp filter used by default. Filters available: ramp, shepp-logan, cosine, hamming, hann Assign None to use no filter.
interpolation : str, optional (default linear)
Interpolation method used in reconstruction. Methods available: nearest, linear.
Returns : output : ndarray
Reconstructed image.
Notes
It applies the fourier slice theorem to reconstruct an image by multiplying the frequency domain of the filter with the FFT of the projection data. This algorithm is called filtered back projection.
probabilistic_hough¶
- skimage.transform.probabilistic_hough(img, threshold=10, line_length=50, line_gap=10, theta=None)¶
Performs a progressive probabilistic line Hough transform and returns the detected lines.
Parameters : img : (M, N) ndarray
Input image with nonzero values representing edges.
threshold : int
Threshold
line_length : int, optional (default 50)
Minimum accepted length of detected lines. Increase the parameter to extract longer lines.
line_gap : int, optional, (default 10)
Maximum gap between pixels to still form a line. Increase the parameter to merge broken lines more aggresively.
theta : 1D ndarray, dtype=double, optional, default (-pi/2 .. pi/2)
Angles at which to compute the transform, in radians.
Returns : lines : list
List of lines identified, lines in format ((x0, y0), (x1, y0)), indicating line start and end.
References
[R52] C. Galamhos, J. Matas and J. Kittler,”Progressive probabilistic Hough transform for line detection”, in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1999.
radon¶
- skimage.transform.radon(image, theta=None)¶
Calculates the radon transform of an image given specified projection angles.
Parameters : image : array_like, dtype=float
Input image.
theta : array_like, dtype=float, optional (default np.arange(180))
Projection angles (in degrees).
Returns : output : ndarray
Radon transform (sinogram).
swirl¶
- skimage.transform.swirl(image, center=None, strength=1, radius=100, rotation=0, output_shape=None, order=1, mode='constant', cval=0)¶
Perform a swirl transformation.
Parameters : image : ndarray
Input image.
center : (x,y) tuple or (2,) ndarray
Center coordinate of transformation.
strength : float
The amount of swirling applied.
radius : float
The extent of the swirl in pixels. The effect dies out rapidly beyond radius.
rotation : float
Additional rotation applied to the image.
Returns : swirled : ndarray
Swirled version of the input.
warp¶
- skimage.transform.warp(image, reverse_map, map_args={}, output_shape=None, order=1, mode='constant', cval=0.0)¶
Warp an image according to a given coordinate transformation.
Parameters : image : 2-D array
Input image.
reverse_map : callable xy = f(xy, **kwargs)
Reverse coordinate map. A function that transforms a Px2 array of (x, y) coordinates in the output image into their corresponding coordinates in the source image. Also see examples below.
map_args : dict, optional
Keyword arguments passed to reverse_map.
output_shape : tuple (rows, cols)
Shape of the output image generated.
order : int
Order of splines used in interpolation. See scipy.ndimage.map_coordinates for detail.
mode : string
How to handle values outside the image borders. See scipy.ndimage.map_coordinates for detail.
cval : string
Used in conjunction with mode ‘constant’, the value outside the image boundaries.
Examples
Shift an image to the right:
>>> from skimage import data >>> image = data.camera() >>> >>> def shift_right(xy): ... xy[:, 0] -= 10 ... return xy >>> >>> warp(image, shift_right)
